In this article we will learn everything about the life of Chandrasekhar Venkat (CV) Raman, Raman Effect on Raman Spectroscopy and Raman Scattering in detail. Useful for graduate and undergraduate students.

Sir Chandrasekhar Venkat Raman, also known as Sir CV Raman, was a Physicist, Mathematician and a Nobel Laureate. Venkat (his first name) was Tamil Brahmin and was the second of the eight children of his parents.
He was born at Thiruvanaikaval, near Tiruchirappalli on 7th November 1888. He was the second of their eight children. His father was a lecturer in mathematics and physics which helped him aspire to careers in the same fields.
Here is how his life progressed:
- At an early age, Raman moved to Visakhapatnam.
- Started studying in St. Aloysius Anglo-Indian High School.
- After his graduation he was selected into government services where he worked for years.
- In 1917, Raman resigned from his government service and took up the newly created Palit Professorship in Physics at the University of Calcutta at the age of 28.
- On February 28, 1928, (the reason National Science Day is celebrated in India) through his experiments on the scattering of light, he discovered the Raman effect. C. V. Raman was awarded the 1930 Physics Nobel Prize for this.
- C.V Raman & Bhagavantam, discovered the quantum photon spin in 1932, which further confirmed the quantum nature of light.
Understanding Raman Effect
Before 1928, infrared spectroscopy was needed to study vibrational & rotational properties of molecules. But after the discovery of Raman Effect, molecules could be excited using visible light spectrum and their properties could be studied more conveniently.
According to Consumer Epic, the Raman effect was first predicted by A. Smekal (1923) and further work was done by Kramers and Heisenberg, (1925) and Dirac (1927). The first experimental evidence for the inelastic scattering of light by molecules such as liquids was observed by Raman and Krishnan in 1928.
It was recognized immediately by Raman that he was dealing with a new phenomenon of a fundamental character in light scattering, something analogous to the Compton effect.
In order to establish its identity, Raman employed a mercury arc and a spectrograph to record the spectrum of the scattered light.
He then made the startling observation that when any transparent substance (be it solid, liquid, or gas) was illuminated by a mercury arc lamp, and the light scattered by the medium was analyzed with the aid of a spectrograph, the spectrum of the scattered light exhibited over and above the lines present in the spectrum of the mercury arc light; either new lines or, in some cases, bands and generally also unresolved continuous radiation shifted from the present line to different extents. The unmodified radiation constituted Rayleigh scattering. Source
Raman Spectroscopy
Definition: Spectroscopy is a branch of science studying the interaction of electromagnetic radiation with matter, with the object of determining the nature of the matter in question. The intensity (power) of this radiation as a function of wavelength, frequency, or energy is called the “spectrum”.
In contrast to other conventional branches of spectroscopy, Raman spectroscopy deals with the scattering of light & not with its absorption.

Chandrasekhar Venkat Raman discovered in 1928 that if light of a definite frequency is passed through any substance in gaseous, liquid or solid state, the light scattered at right angles contains radiation not only of the original frequency (Rayleigh Scattering) but also of some other frequencies which are generally lower but occasionally higher than the frequency of the incident.
The phenomenon of scattering of light by a substance when the frequencies of radiation scattered at right angles are different (generally lower and only occasionally higher) from the frequency of the incident light, is known as Raman Scattering or Raman effect.
The lines of lower frequencies are known as Stokes lines, while those of higher frequencies are called anti-stokes lines.
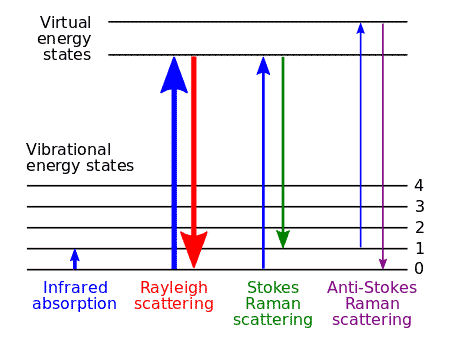
If $f$ is the frequency of the incident light & $f'$ that of a particular line in the scattered spectrum, then the difference $f-f'$ is known as the Raman Frequency. This frequency is independent of the frequency of the incident light. It is constant and is characteristic of the substance exposed to the incident light.
A striking feature of Raman Scattering is that Raman Frequencies are identical, within the limits of experimental error, with those obtained from rotation-vibration (infrared) spectra of the substance.
The Raman scattering takes place due to inelastic collision between photons and electrons. The difference in energy between incident photon and emitted photons generates Raman lines.
Here is a video guide for Raman Spectroscopy by Practical Ninja:
Advantages of Raman Effect
- Raman Spectroscopy can be used not only for gases but also for liquids & solids for which the infrared spectra are so diffuse as to be of little quantitative value.
- Raman Effect is exhibited not only by polar molecules but also by non-polar molecules such as $O_2$, $N_2$, $Cl_2$ etc.
- The rotation-vibration changes in non-polar molecules can be observed only by Raman Spectroscopy.
- The most important advantage of Raman Spectra is that it involves measurement of frequencies of scattered radiations, which are only slightly different from the frequencies of incident radiations. Thus, by appropriate choice of the incident radiations, the scattered spectral lines are brought into a convenient region of the spectrum, generally in the visible region where they are easily observed. The measurement of the corresponding infrared spectra is much more difficult.
- It uses visible or ultraviolet radiation rather than infrared radiation.
Usage
- Investigation of biological systems such as polypeptides and the proteins in aqueous solutions.
- Determination of the structures of molecules.
Classical Theory of Raman Effect
The classic theory of Raman effect, also called the polarizability theory, was developed by G. Placzek in 1934. I shall discuss it briefly here.
When a photon interacts with a molecule it will cause the electrons and protons to move and this will induce an oscillating dipole. This dipole will then radiate photons of different frequencies.
It is known from electrostatics that the electric field $ E $ associated with the electromagnetic radiation induces a dipole moment $ \mu $ in the molecule, given by
$ \mu = \alpha E $ .......(1)
where $ \alpha $ is the polarizability of the molecule. The electric field vector $ E $ itself is given by
$ E = E_0 \sin \omega t = E_0 \sin 2\pi \nu t $ ......(2)
where $ E_0 $ is the amplitude of the vibrating electric field vector and $ \nu $ is the frequency of the incident light radiation.
Thus, from equations (1) & (2),
$ \mu= \alpha E_0 \sin 2\pi \nu t $ .....(3)
Such an oscillating dipole emits radiation of its own oscillation with a frequency $ \nu $ , giving the Rayleigh scattered beam. If, however, the polarizability varies slightly with molecular vibration, we can write
$ \alpha =\alpha_0 + \frac {d \alpha} {dq} q $ .....(4)
where the coordinate q describes the molecular vibration.
We can also write $q$ as:
$ q=q_0 \sin 2\pi \nu_m t $ .....(5)
Where $ q_0$ is the amplitude of the molecular vibration and $ \nu_m $ is its (molecular) frequency.
From equations. 4 & 5, we have
$ \alpha =\alpha_0 + \frac {d\alpha} {dq} q_0 \sin 2\pi \nu_m t $ .....(6)
Substituting for $ alpha $ in (3), we have
$ \mu= \alpha_0 E_0 \sin 2\pi \nu t + \frac {d\alpha}{dq} q_0 E_0 \sin 2\pi \nu t \sin 2\pi \nu_m t $ .......(7)
Making use of the trigonometric relation $ \sin x \sin y = \frac{1}{2} [\cos (x-y) -\cos (x+y) ] $ this equation reduces to:
$ \mu= \alpha_0 E_0 \sin 2\pi \nu t + \frac {1}{2} \frac {d\alpha}{dq} q_0 E_0 [\cos 2\pi (\nu - \nu_m) t - \cos 2\pi (\nu+\nu_m) t] $ ......(8)
Thus, we find that the oscillating dipole has three distinct frequency components:
- The exciting frequency $ \nu $ with amplitude $ \alpha_0 E_0 $
- $ \nu - \nu_m $
- $ \nu + \nu_m $ (2 & 3 with very small amplitudes of $ \frac {1}{2} \frac {d\alpha}{dq} q_0 E_0 $
Hence, the Raman spectrum of a vibrating molecule consists of a relatively intense band at incident frequency and two very weak bands at frequencies slightly above and below that of the intense band.
If, however, the molecular vibration does not change the polarizability of the molecule then $ (d\alpha / dq )=0$ so that the dipole oscillates only at the frequency of the incident (exciting) radiation. The same is true for molecular rotation. We conclude that for a molecular vibration or rotation to be active in the Raman Spectrum, it must cause a change in the molecular polarizability, i.e., $ d\alpha/dq \ne 0$ .......(9)
Homo-nuclear diatomic molecules such as $ \mathbf {H_2 , N_2 , O_2} $ which do not show IR Spectra since they don't possess a permanent dipole moment, do show Raman spectra since their vibration is accompanied by a change in polarizability of the molecule. As a consequence of the change in polarizability, there occurs a change in the induced dipole moment at the vibrational frequency.